Home -> Solved problems -> Derivative of exponential x
Proof: Derivative of exponential x from first principles
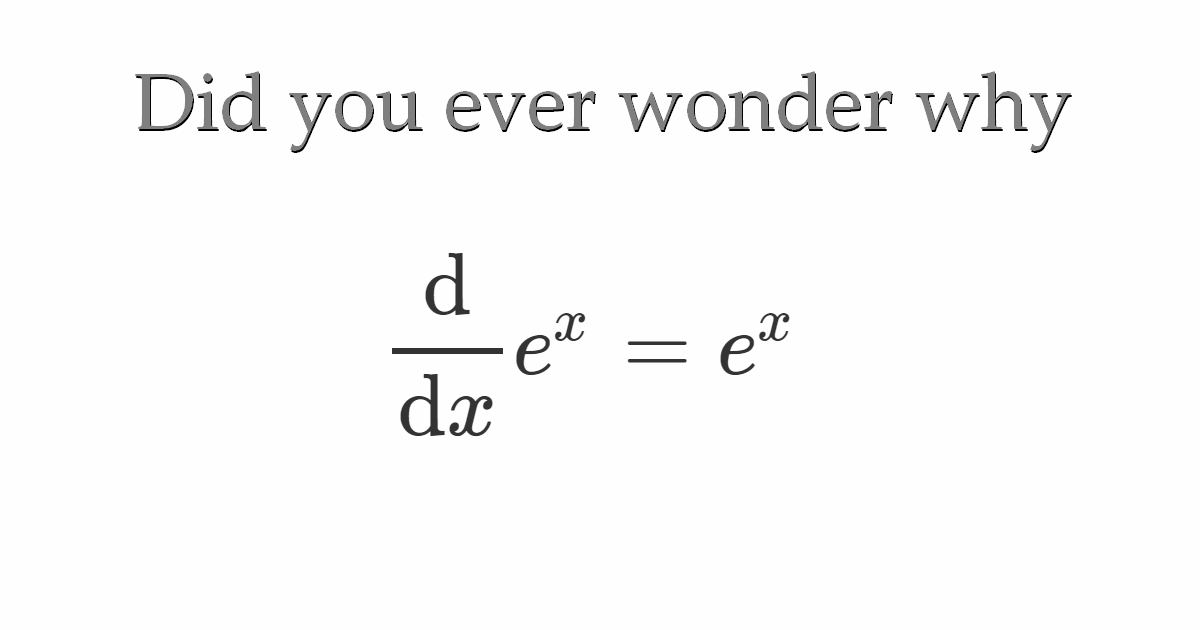
Solution
To start, we define a function \(f\) such that \[f\left(x\right)=e^{x}\;\;\;\;\;\;\;,\; x\epsilon\mathbb{C}\] By definition \[e^{x}=\lim_{n \rightarrow \infty}\left(1+\frac{x}{n}\right)^{n}\] Now let’s calculate the derivative of the function f \[f’\left(x\right)=\lim_{\delta x \rightarrow 0}\frac{f\left(x+\delta x\right)-f\left(x\right)}{\delta x}\] \[=\lim_{\delta x \rightarrow 0}\frac{e^{x+\delta x}-e^{x}}{\delta x}\] \[=\lim_{\delta x \rightarrow 0}\lim_{n \rightarrow \infty}\frac{1}{\delta x}\left(\left(1+\frac{x+\delta x}{n}\right)^{n}-e^{x}\right)\] \[=\lim_{\delta x \rightarrow 0}\lim_{n \rightarrow \infty}\frac{1}{\delta x}\left(\left(\left(1+\frac{x}{n}\right)+\frac{\delta x}{n}\right)^{n}-e^{x}\right)\] Now let’s use the Binomial theorem, according to the theorem we can expand any non-negative power of \(a+b\) into a sum \[\color{olive} {(a+b)^{n}=\left(\begin{array}{c}n\\ 0\end{array}\right)a^{n}b^{0}+\left(\begin{array}{c}n\\ 1\end{array}\right)a^{n-1}b^{1}+\left(\begin{array}{c}n\\ 2\end{array}\right)a^{n-2}b^{2}+\cdots +\left(\begin{array}{c}n\\ n-1\end{array}\right)a^{1}b^{n-1}+\left(\begin{array}{c}n\\ n\end{array}\right)a^{0}b^{n}}\] Therefore \[f’ \left(x\right)=\lim_{\delta x \rightarrow 0}\lim_{n \rightarrow \infty}\frac{1}{\delta x}\left(\left(1+\frac{x}{n}\right)^{n}+\left(\begin{array}{c}n\\ 1\end{array}\right)\left(1+\frac{x}{n}\right)^{n-1}\left(\frac{\delta x}{n}\right)+\cdot\cdot\cdot+\left(\frac{\delta x}{n}\right)^{n}-e^{x}\right)\] \[=\lim_{\delta x \rightarrow 0}\lim_{n \rightarrow \infty}\left(\frac{\left(1+\frac{x}{n}\right)^{n}-e^{x}}{\delta x}+\left(\begin{array}{c}n\\ 1\end{array}\right)\left(1+\frac{x}{n}\right)^{n-1}\left(\frac{1}{n}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)\left(1+\frac{x}{n}\right)^{n-2}\left(\frac{\delta x}{n^{2}}\right)+\cdot\cdot\cdot+\frac{\left(\delta x\right)^{n-1}}{n^{n}}\right)\] \[=\left(\lim_{\delta x \rightarrow 0}\frac{e^{x}-e^{x}}{\delta x}\right)+\lim_{n \rightarrow \infty}\left(\left(\begin{array}{c}n\\ 1\end{array}\right)\left(1+\frac{x}{n}\right)^{n-1}\left(\frac{1}{n}\right)+\left(\begin{array}{c}n\\ 2\end{array}\right)\left(1+\frac{x}{n}\right)^{n-2}\left(\frac{0}{n^{2}}\right)+\cdot\cdot\cdot+\frac{0}{n^{n}}\right)\] \[=\frac{0}{0}+\lim_{n \rightarrow \infty}\left(\left(\begin{array}{c}n\\ 1\end{array}\right)\left(1+\frac{x}{n}\right)^{n-1}\left(\frac{1}{n}\right)+0+\cdot\cdot\cdot+0\right)\] We have an indeterminate form \(\frac{0}{0}\), so to fix that we use Hospital’s Rule, thus \[f’ \left(x\right)=\left(\lim_{\delta x \rightarrow 0}\frac{0}{1}\right)+\lim_{n \rightarrow \infty}\left(\begin{array}{c}n\\ 1\end{array}\right)\left(1+\frac{x}{n}\right)^{n-1}\left(\frac{1}{n}\right)\] \[=\lim_{n \rightarrow \infty}\left(\begin{array}{c}n\\ 1\end{array}\right)\left(\frac{1}{n}\right)\left(1+\frac{x}{n}\right)^{n-1}\] We have \[\left(\begin{array}{c}n\\ 1\end{array}\right)\left(\frac{1}{n}\right)=\frac{n!}{1!\left(n-1\right)!}=n\left(\frac{1}{n}\right)=1\] Finally \[f’\left(x\right)=\lim_{n \rightarrow \infty}\left(1+\frac{x}{n}\right)^{n-1}\] \[=\lim_{n \rightarrow \infty}\frac{\left(1+\frac{x}{n}\right)^{n}}{\left(1+\frac{x}{n}\right)}\] \[=\frac{e^{x}}{1}=e^{x}\] Hence \[\large \frac{\text{d}}{\text{d}x}e^{x}=e^{x}\]
Home -> Solved problems -> Derivative of exponential x
Related Topics
Home -> Solved problems -> Derivative of exponential x
Share the solution: Derivative of exponential x