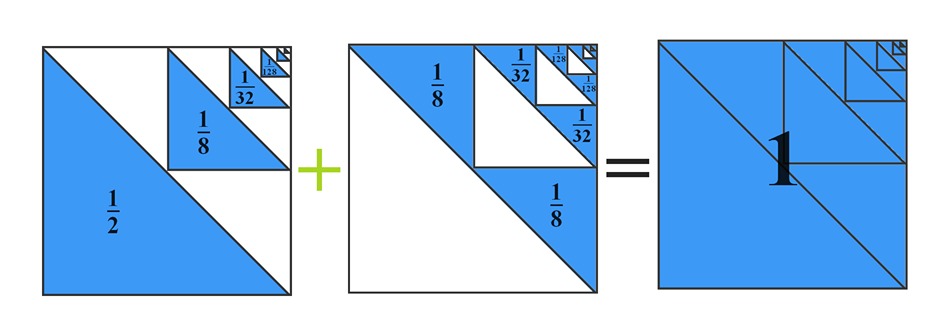
Proof without words

Proof without words: \(\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\cdots=1\)

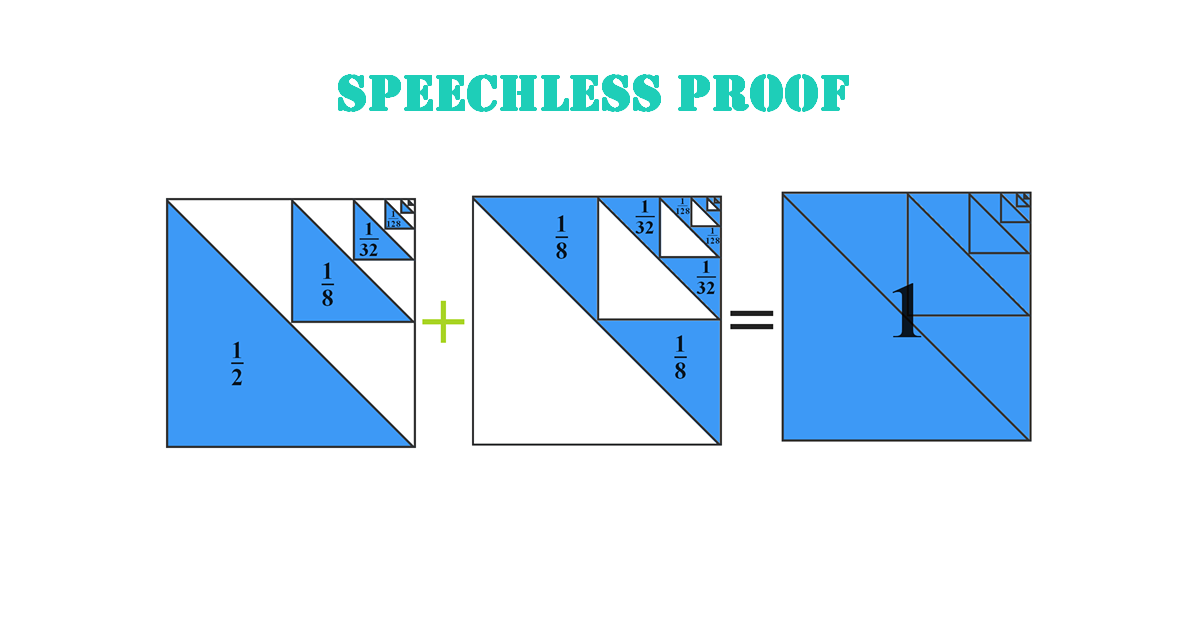
Explanation

This infinite series visual proof demonstrates how the sum of \( \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \cdots \) equals 1. Using simple geometric shapes, this speechless proof illustrates the concept of infinite sums without words, making mathematics both visual and intuitive.

The proof is part of the Proof Without Words series on Art Of Mathematics, which provides elegant visual explanations for important mathematical concepts. By showing each fraction as a geometric area, learners can immediately see why the sum converges to 1, reinforcing understanding without relying on symbolic calculation alone.

Such speechless proofs are not only educational but also enhance visual intuition in mathematics, helping students grasp abstract ideas quickly and enjoyably.

Each colored section in the figure represents a fraction of the whole, showing how the pieces fit together perfectly. This visual approach helps understand the convergence of infinite series in a simple and elegant way. Explore other proof without words examples on this site to discover more fascinating mathematics concepts made visual.

We can extract from the next figure the following infinite sum:

\[ \frac{1}{2} + \frac{1}{8} + \frac{1}{32} + \frac{1}{128} + \cdots \]

The same thing for the next figure

\[\frac{2}{8}+\frac{2}{32}+\frac{2}{128}+\frac{2}{512}+\cdots\]

Now, let’s focus on the next figure to find out the result we get

\[ \begin{aligned} &\left(\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+\frac{1}{128}+\cdots\right)+\left(\frac{2}{8}+\frac{2}{32}+\frac{2}{128}+\frac{2}{512}+\cdots\right)=1 \\ &\left(\frac{1}{2}+\frac{1}{8}+\frac{1}{32}+\frac{1}{128}+\cdots\right)+\left(\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\frac{1}{256}+\cdots\right)=1 \\ &\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}+\frac{1}{256}+\cdots=1 \\ &\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\frac{1}{2^{4}}+\frac{1}{2^{5}}+\frac{1}{2^{6}}+\frac{1}{2^{7}}+\frac{1}{2^{8}}+\cdots=1 \end{aligned} \]

Proof without words: \(\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\cdots=1\)

Explanation

Related Topics