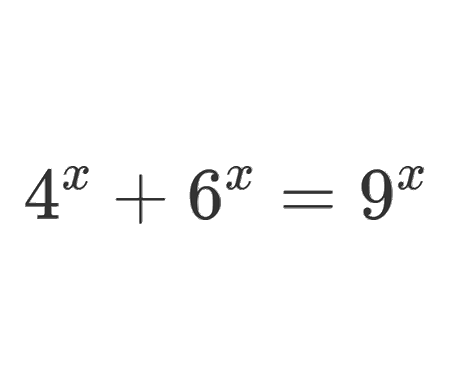"100 doors" problem
Home -> Solved problems -> “100 doors” problem

Solution
Restating the Problem:
- There are 100 doors in a row.
- Initially, all the doors are closed.
- You make 100 passes by the doors.
- On the first pass, you visit every door and toggle (open or close) each one.
- On the second pass, you visit every second door (i.e., doors 2, 4, 6, …), and toggle them.
- On the third pass, you visit every third door (i.e., doors 3, 6, 9, …), and toggle them.
- You continue this process until the 100th pass, where you only toggle the 100th door.
Key Insight:
For any given door, it is toggled (open or closed) when you visit it. You visit a door when the pass number is a divisor of the door number. For example:
- Door 12 is toggled on passes 1, 2, 3, 4, 6, and 12, because these numbers divide 12 evenly.
Initially, all doors are closed. For a door to end up open, it must be toggled an odd number of times (since it starts closed and toggling an odd number of times will leave it open).
When Does a Door Get Toggled an Odd Number of Times?
A door is toggled on passes that correspond to its divisors. Most numbers have divisors that come in pairs. For example:
- The divisors of 12 are 1, 12, 2, 6, 3, 4, and they pair up like this: (1, 12), (2, 6), (3, 4).
So, the number 12 has an even number of divisors, which means door 12 will be toggled an even number of times and will therefore remain closed.
However, for numbers that are perfect squares, one of the divisors is repeated. For example:
- The divisors of 9 are 1, 9, and 3, but notice that 3 is repeated (since 3 × 3 = 9).
In this case, there is an odd number of divisors (1, 3, and 9), meaning that door 9 will be toggled an odd number of times and will remain open.
Conclusion:
The doors that remain open are those whose numbers are perfect squares, because only perfect squares have an odd number of divisors.
Thus, the doors that remain open are:
- Door 1 (since 1 = 1²)
- Door 4 (since 4 = 2²)
- Door 9 (since 9 = 3²)
- Door 16 (since 16 = 4²)
- Door 25 (since 25 = 5²)
- Door 36 (since 36 = 6²)
- Door 49 (since 49 = 7²)
- Door 64 (since 64 = 8²)
- Door 81 (since 81 = 9²)
- Door 100 (since 100 = 10²)
Final Answer:
The doors that remain open after 100 passes are the ones with numbers that are perfect squares: 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100.
Mathematical Explanation:
- A number n has divisors that come in pairs (d1,d2), where d1×d2=n.
- For non-perfect squares, the divisors come in even pairs, meaning the door will be toggled an even number of times and remain closed.
- For perfect squares, there is one divisor that repeats, which results in an odd number of toggles, leaving the door open.
This solution encourages exploration of divisibility and introduces concepts like perfect squares and factors in a logical and engaging manner!
Home -> Solved problems -> “100 doors” problem