Proof without words: The Pythagorean Theorem
Explanation
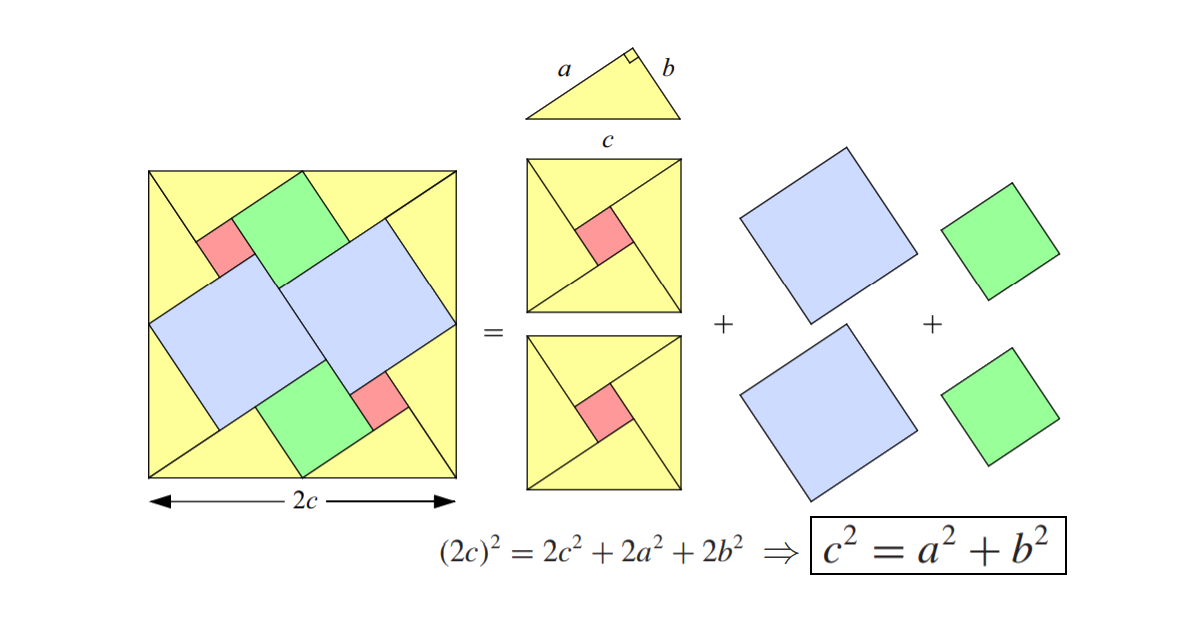
We start with a right triangle and duplicate the yellow triangle to obtain eight similar triangles. By arranging these triangles, we form the sides of a square as shown in the figure. Next, we gradually fill the white spaces by adding two blue squares, followed by two green squares of side \(b\), and finally the two remaining red squares. This assembly shows that the area of the largest square is equal to the sum of the areas of the smaller squares, providing a clear, visual proof of the Pythagorean Theorem.
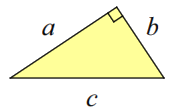
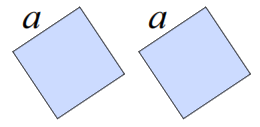
We take a right triangle with sides \(a\), \(b\) and \(c\)
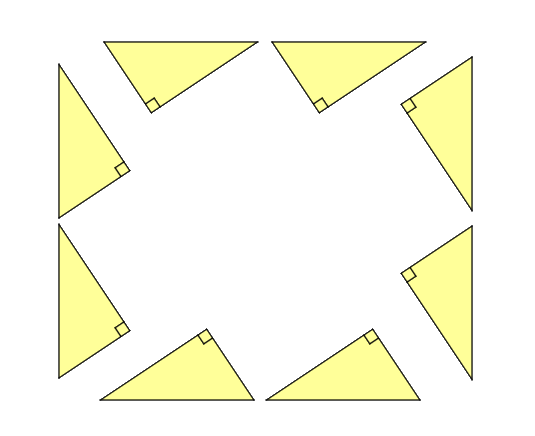
Then we duplicate the yellow triangle to get 8 similar triangles
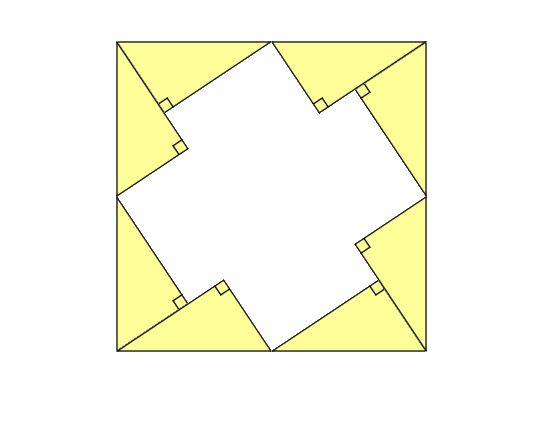
Now we assemble the triangles to get the sides of a square like it is shown in the next figure
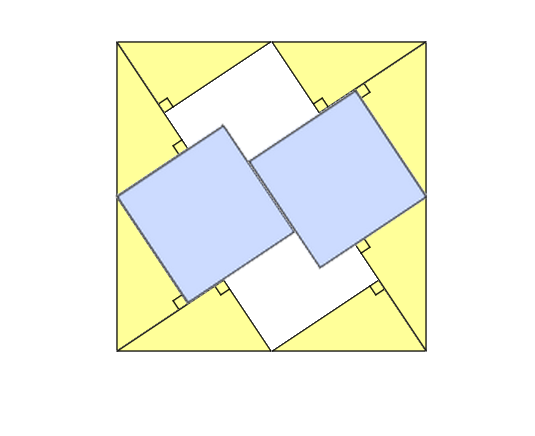
Next, let’s try to fill the white space until we get a filled square. We start by adding 2 blue squares of the same side within the previous figure. We get
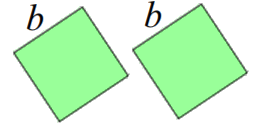
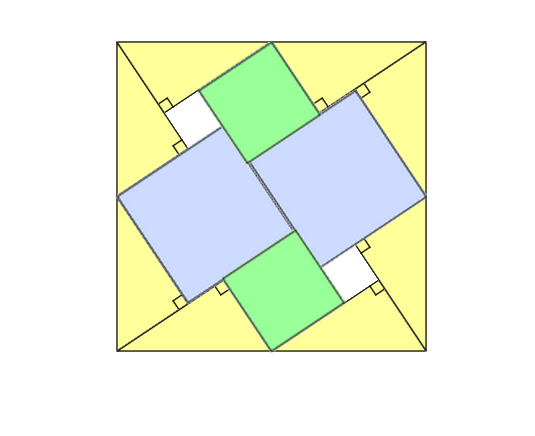
Then, we add 2 green squares of side b
Finally, we fill the rest by adding the two last squares of the same side coloured in red
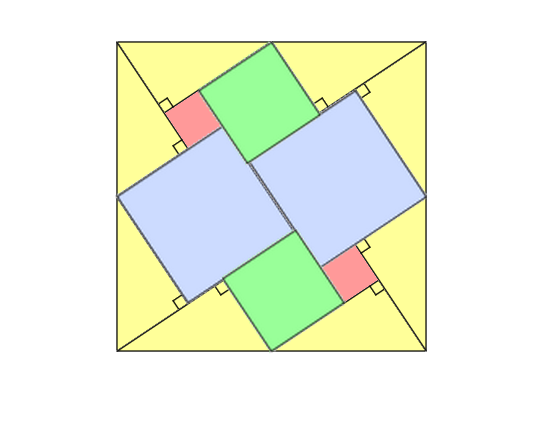
We can divide the area of the biggest square into these parts to get our final result.
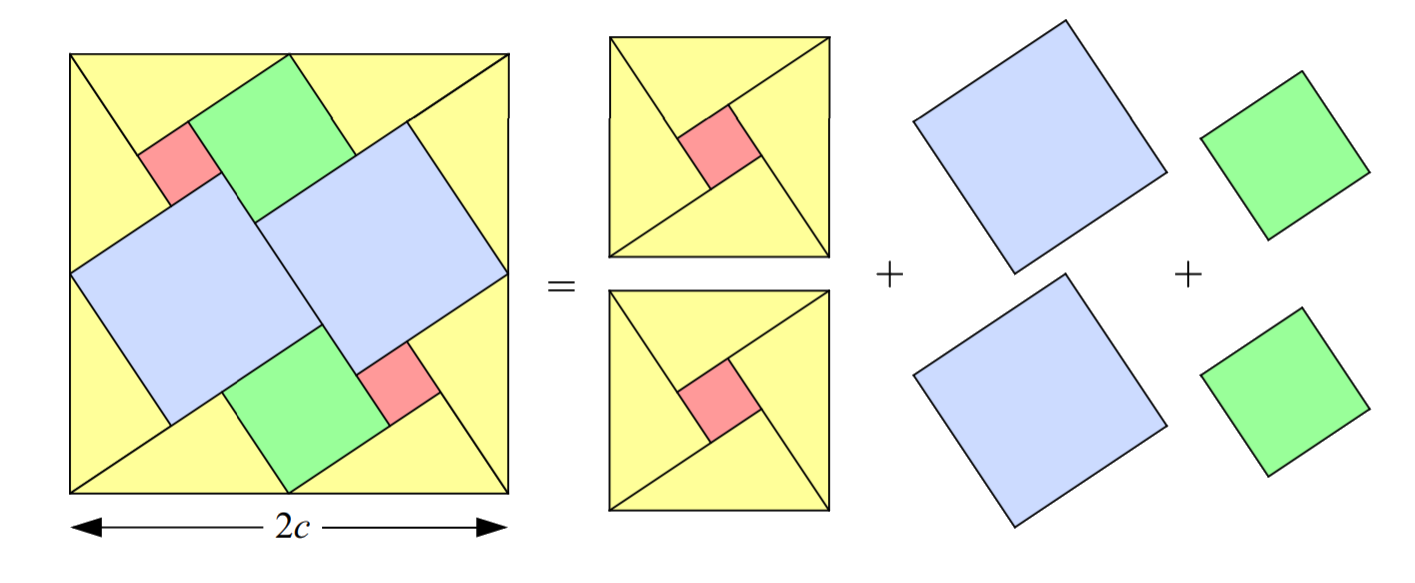
\[\huge \left(2c\right)^{2}=2c^{2}+2a^{2}+2b^{2}\Rightarrow c^{2}=a^{2}+b^{2}\]
